【その他】是非読んで頂きたい「ゲームの面白さ」についての研究の話

先日、とある大学院の先生に教えていただいた話です。
あまりに感動したので是非共有させていただきます。
この記事の前半部分は引用についての説明と論文の紹介になります。

ただし、正確な理論の紹介や前提条件の定義付けは直接論文を読まれたほうが良いと思うので、ここでは省かせていただきます。

自意識過剰かもしれませんが、引用先の明示なくTwitterやFacebookなどで図表だけ拡散するのは絶対にやめて下さい。皆さんが著作権法違反になる場合がございます。
また、もちろん先生への誹謗中傷も厳禁です。
正しい議論の形なら喜んで受けてくださると思いますが…笑

以下の文章で論文の引用の仕方など間違いがあれば指摘していただきたいです。
引用に際しまして、以下のページを参考にしました。
論文の「引用」と著作権法
http://blogs.itmedia.co.jp/natsume/2013/09/2013.html

ゲーム研究のいま(サービスとしてのゲーム)-飯田弘之
http://ci.nii.ac.jp/naid/110009554508

An Application of Game-Refinement Theory to Mah Jong-飯田弘之
http://link.springer.com/chapter/10.1007%2F978-3-540-28643-1_41

以下の文章と図表は、ゲーム研究のいま(サービスとしてのゲーム)からの引用です。
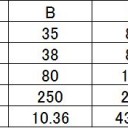
ただし、図表２は麻雀の項を追加するため、書き足しております。

ゲームの平均可能手数B と平均終了手数D に対して，
D の値が0.07 前後になるようにゲームが進化してき
たことがわかっている（図4）。
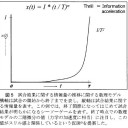
試合結果が終了間際まで判らないとき，ハラハラドキド
キしたスリル感あふれる試合展開となる。筆者はこのよう
な試合進行パターンに着目し，試合結果に関する情報の時
間変化の数理モデル3）を提案した。終了問際での二階微分
（力学の加速度に相当） の値，つまり√B/Dの値がスリル
感の大小に対応する（図5）。
　様々なゲームでこの値を調べたところ，数百年以上の長
い年月を生き残っているゲームでは，ほぼ同じ値になって
いることがわかった。人類の知性がそれぞれ異なる地域で，
あるいは，それぞれ異なるゲームで同じ程度のスリル感を
求めてきた結果であると考えている。
この考え方は，ゲームのルールの進化論的変遷をうまく説明できることがわ
かっている。

ただし、図4は1枚目の画像、図5は2枚目の画像を示しております。


この文章はつまり、「長く愛されているテーブルゲームは取り得る選択肢数の平方根を終了までの手数で割ると0.075前後になる。また、そうなるようにルールが変化してきた。」

飯田先生はこの論文の本質はこの部分ではなく、これがどんな一般性を持つか、さらにどう活かすかという点にあるとおっしゃっていましたが、私にはこの美しさに凄く感動しました。

さらにこれはテーブルゲームだけでなく、スポーツやテレビゲームなども同じ傾向があるようで、先生は現在も研究を行っていらっしゃいます。

多少別の指標も必要であるそうですが、自分としてはやはりカードゲームでこの理論を適応させてみたいですね。

ゲームを楽しむ人、楽しませる人、ゲームに携わる人全てに是非知っていただきたいなと思い記事にさせていただきました。